广度优先搜索

案例1：队列实现迷宫问题

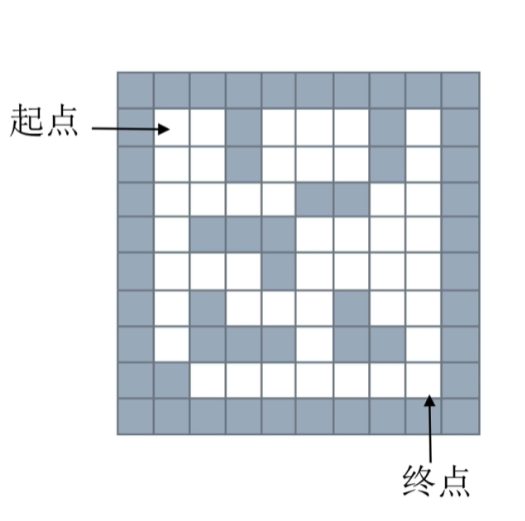
思路 ：从起点开始，分成多步（上、下、左、右），并用队列记录这些步。当从某个点走到下一个点时，对该点 出队 ，并将下一步的可能点进队（可能是多个）。最终先到达终点的就是最短路径。每次出队进队时，都需要记录该点是由那个点走来的，这样便可以回溯，从而找到所求路径。

代码实现

from collections import deque
def solve(maze , start , end):
    queue = deque(maxlen=100)
    queue.append(start)
    possibleStep = [
        lambda i : [i[0] - 1    ,   i[1]    ] ,
        lambda i : [i[0]        ,   i[1] + 1] ,
        lambda i : [i[0] + 1    ,   i[1]    ] ,
        lambda i : [i[0]        ,   i[1] - 1] ,
    ]
    traceBack = {}
    traceBack[str(start)] = None
    # 标记起点
    maze[start[0]][start[1]] = 1
    # 队列找终点
    while True:
        if end in queue:
            break
        else:
            # 原位置出队列
            originCoord = queue.popleft()
            # 找下一个可能的位置
            for i in possibleStep:
                nextCoord = i(originCoord)
                if maze[nextCoord[0]][nextCoord[1]] == 0:   # 可走
                    # 记录进回溯字典
                    # 下一步为键，原步为值
                    traceBack[str(nextCoord)] = str(originCoord)
                    # 下一步入队列
                    queue.append(nextCoord)
                    # 标记为走过
                    maze[nextCoord[0]][nextCoord[1]] = 1
    # 回溯路径
    nowCoord = str(end)
    res = []
    while nowCoord != None:
        res.append(nowCoord)
        nowCoord = traceBack[nowCoord]
    return res