深度优先搜索

迷宫问题——栈实现

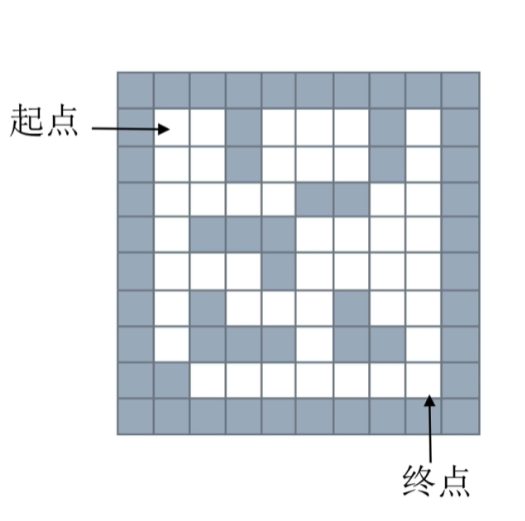
思路 ：

使用栈记录路径，每走一步就push入栈，并按一定顺序搜索可走的下一步，直到遇到无路可走。无路可走时，依次出栈，知道遇到最近的一个存在可走路径的点（将走过的路标记），然后从该点开始继续上述循环。最后便能找到一条走出迷宫的路径。

测试输入样例：

maze = [
    [1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1] ,
    [1 , 0 , 0 , 1 , 0 , 0 , 0 , 1 , 0 , 1] ,
    [1 , 0 , 0 , 1 , 0 , 0 , 0 , 1 , 0 , 1] ,
    [1 , 0 , 0 , 0 , 0 , 1 , 1 , 0 , 0 , 1] ,
    [1 , 0 , 1 , 1 , 1 , 0 , 0 , 0 , 0 , 1] ,
    [1 , 0 , 0 , 0 , 1 , 0 , 0 , 0 , 0 , 1] ,
    [1 , 0 , 1 , 0 , 0 , 0 , 1 , 0 , 0 , 1] ,
    [1 , 0 , 1 , 1 , 1 , 0 , 1 , 1 , 0 , 1] ,
    [1 , 1 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 1] ,
    [1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1]
]
start = [1 , 1]
end =   [8 , 8]

# python
class Stack:
    def __init__(self):
        self.data = []

    def push(self , element):
        self.data.append(element)

    def pop(self):
        if self.is_empty():
            raise IndexError("Stack is empty.")
        return self.data.pop()

    def get_top(self) -> any:
        if self.is_empty():
            raise IndexError("Stack is empty.")
        return self.data[-1]

    def is_empty(self) -> bool:
        return len(self.data) == 0

    def print_stack(self):
        print(self.data)
        return self.data

def solve(maze , start , end):
    # 搜索顺序
    searchOrder = [[-1 ,  0] , # 上
                   [0  ,  1] , # 右
                   [1  ,  0] , # 下
                   [0  , -1] , # 左
                   ]
    pathStack = Stack()
    pathStack.push(start)
    # 路径算法
    while pathStack.get_top() != end:
        nowCoord = pathStack.get_top()
        # print(nowCoord)
        # 寻找下一个优先的可用路径
        for i in searchOrder:
            nextCoord = [nowCoord[0] + i[0] , nowCoord[1] + i[1]]
            if maze[nextCoord[0]][nextCoord[1]] == 0:
                nowCoord = nextCoord
                break
        else: # 如果没有可用路径，回退找最近一个
            while True:
                # 出栈
                coord = pathStack.get_top()
                # print(coord)
                nextAccessableCoord = None
                # 寻找可走路径
                for i in searchOrder:
                    nextCoord = [coord[0] + i[0] , coord[1] + i[1]]
                    if maze[nextCoord[0]][nextCoord[1]] == 0:
                        nextAccessableCoord = nextCoord
                # 如果找到可以走的路径
                if nextAccessableCoord != None:
                    # 标记为当前坐标以便统一入栈，跳出循环
                    nowCoord = nextAccessableCoord
                    break
                else:
                    # 否则,出栈并继续回退
                    pathStack.pop()
                    continue
        # 走路径：标记目前路径为1，入栈
        maze[nowCoord[0]][nowCoord[1]] = 1
        pathStack.push(nowCoord)
    # 输出结果
    return pathStack.print_stack()

问题 ：无法实现最短路径